
As with any problem, we must decide what lens/perspective we will look at the problem with. Will it be energy or kinematics? In this case both perspectives will work, although energy is more intuitive.
In this problem, energy is conserved as gravity is a conservative force. Normal force does no work as it will be acting perpendicular to the velocity, possibly changing its direction BUT NOT magnitude.

(Notice that mass does not matter in this case. If a physics problem appears to give you too little information, try to solve it algebraically and see if any variables cancel out)
Setting the gravitational potential energy = kinetic energy, we arrive at the final equation. However, we don’t know what the velocity is. How do we solve for it?
We must look at some concepts relating specifically to circular motion. Whenever you encounter a problem with riders inside a roller coaster loop, it will deal with either the top of the loop, the bottom of the loop, or both.
Analyzing the force diagrams of both positions we arrive at:
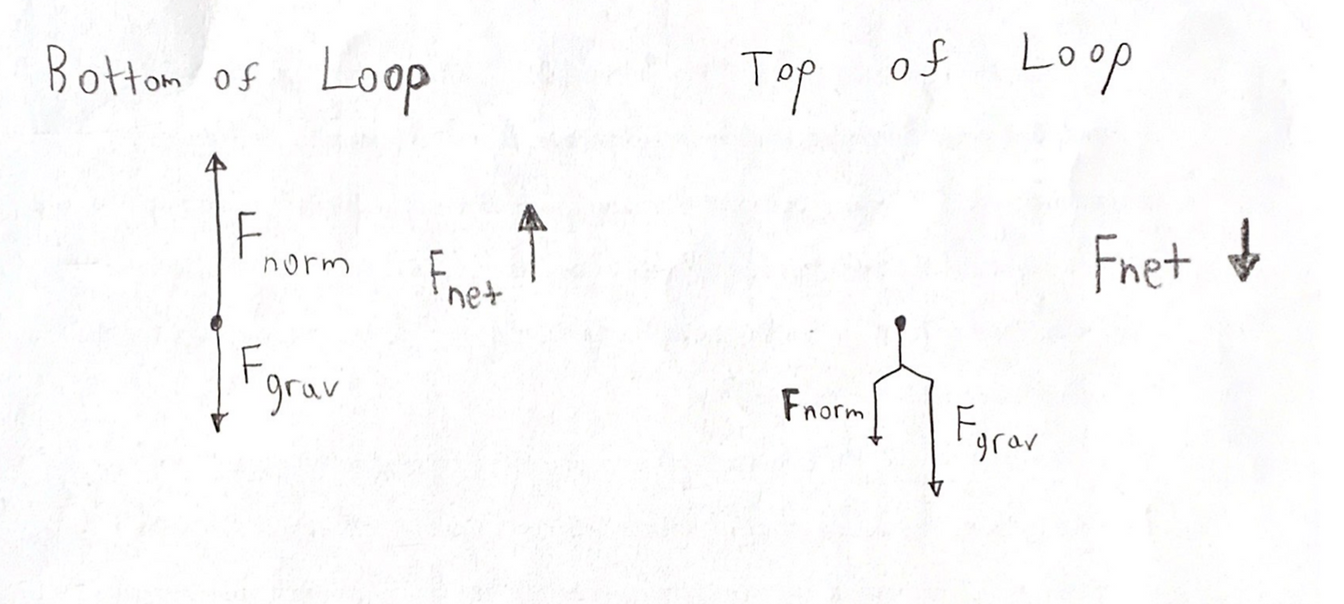
Notice that at the bottom of the loop the forces act in opposite directions and at the top of the loop, the forces act in the same direction. This will affect how net force is calculated.
At the bottom: Fnet = Fnorm – Fgrav
At the top: Fnet = Fnorm + Fgrav
Fnet will always point towards the center of the loop due to circular motion.
For this particular problem, we will be focusing on the top of the loop instead of the bottom as we are aiming to “complete the… loop”. Reaching the bottom should be no problem, but reaching the top takes some calculation.
To relate the net force to velocity, we must also know that:
Centripetal Acceleration = V^2/R (where V is the velocity and R is the radius of the circle)
Using F=MA, we arrive at:
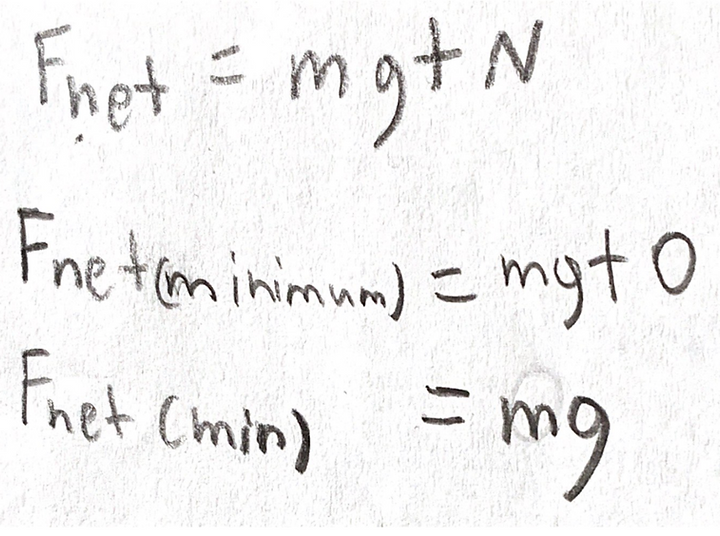
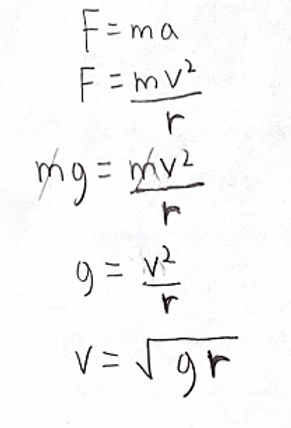
The Fnet in this case is only mg, with no normal force. Mg remains constant regardless of the speed, but normal force can vary from 0 -> infinity. Setting Fnet to its minimum (and thus normal force to its minimum) allows us to solve for the minimum speed required to complete the loop.
Going back to our previous work with energy we arrive at:
However, we aren’t done! We actually calculated for the height above above the roller coaster loop, not from above the ground (as we were working with the top of the loop when we solved for velocity). To solve for the actual initial height of the roller coaster, we must add the height of the roller coaster loop itself, which is the diameter.
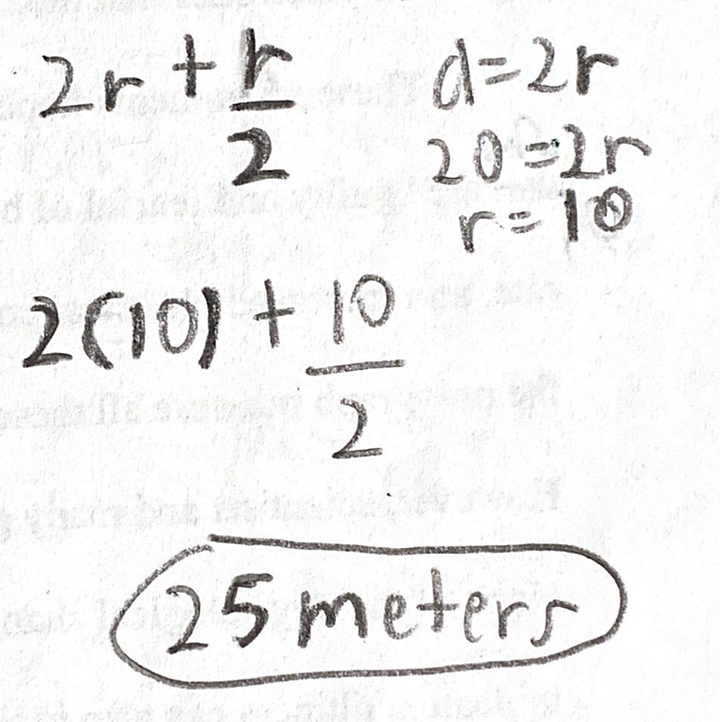
With any kinematics problem, you are aiming to find 3 variables that you know to solve for a fourth unknown variable. In this problem, the knowns and unknown are:
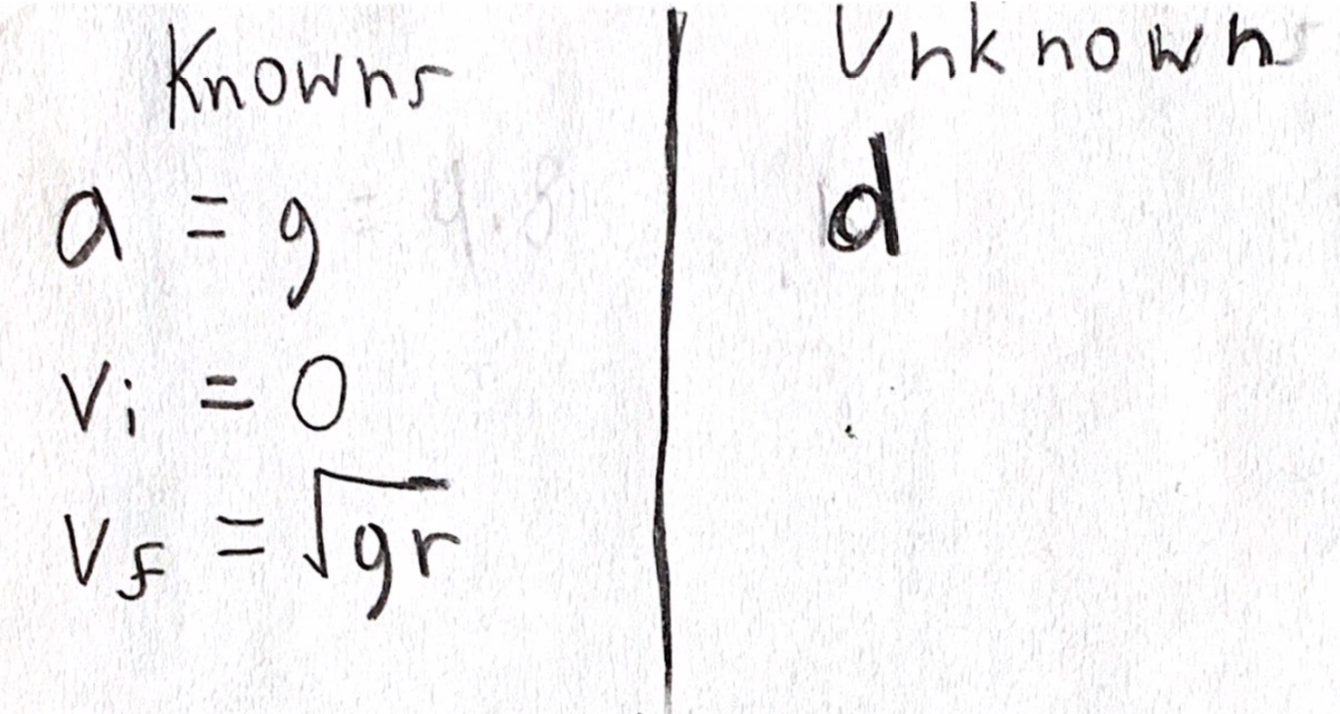
The acceleration in this case is g, not v^2/r, as we evaluating this problem as if the coaster is going straight down to the top of the loop. Because energy is conserved, traveling to the bottom of the loop and back up to the top is mathematically the same as traveling directly to the top of the loop. However, the speed at the top of the loop (Vf) is solved using centripetal motion concepts as discussed in the energy portion.
From here, we pick one of the four kinematics equations that incorporates these variables.
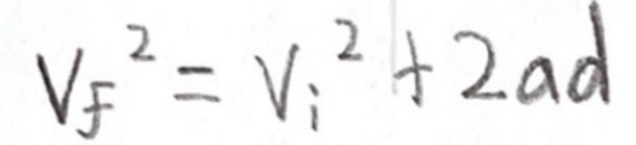
Filling in the variables, we arrive at:
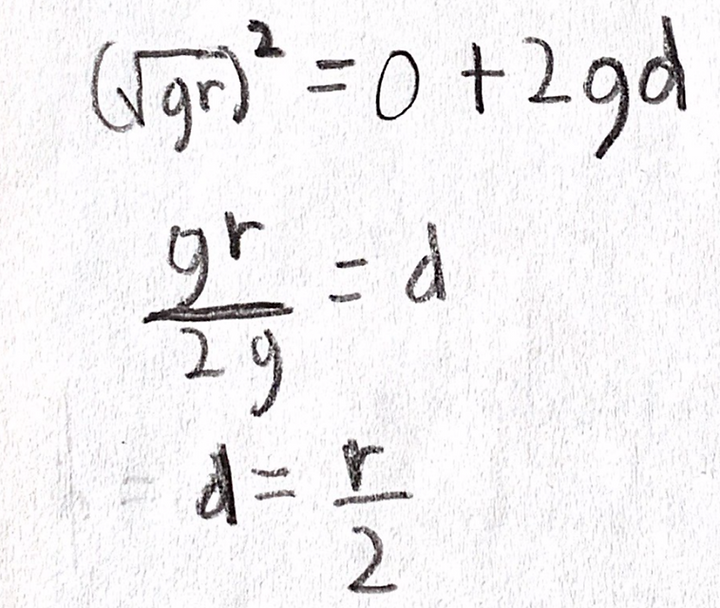
However, like with energy, we must account for the height of the loop. So our final answer = 25 meters.
Overall, the energy perspective is more intuitive because the problem relies of the conservation of energy. Kinematics only works in this case because of the conservation of energy.

